Graphical Method of Solution of a Pair of Linear Equations

For which value of k will the following pair of linear equations have no solution?
$3x + y = 1$,

$(2k -1)x + (k -1)y = 2k + 1$

For the given system of equations, determine the value of $k$ for which the given system has no solution.

$3x-4y+7=0$

$kx+3y-5=0$

The value of $a$ for which the pair of equations $8x+5y=9$ and $ax+10y=15$ has no solution is

Draw graphs of $x+y+3=0$ and $3x-2y+4=0$. Find the coordinates of the point of intersection of lines. Also find the distance of the point of intersection of the lines from the origin in $\mathrm{cm}$.

The pair of equations $y=0\text{ and }y=-7$ has

Find the area of the triangular region whose vertices are the points of intersection of the graphs $2x+y=5, y=x-4$ and $y=5$.

Solve the pair of linear equations in two variables by graphical method.

$3x-4y-2=0$

$2x+3y-7=0$

Which is not a method to find the solution of $2x-3y=9$ and $3x+4y=19$?

The graph of a line represented by the equation $ax+y+8= 0$ is shown in the figure below.

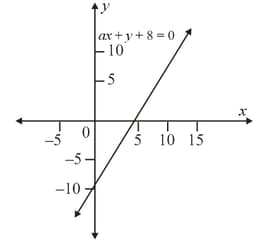
Find the value of $a$. Find the point of intersection of this line with the line represented by the equation $4x-3y-14= 0$.

Show your work.

The pair of linear equations $\frac{3x}{2}+\frac{5y}{3}= 7$ and $9x+10y= 14$ is:

Draw graph:

$\left(i\right) x+y= 5$ $\left(ii\right) 2x-y= 4$

Solve the following system of linear equations graphically: $3𝑥+𝑦-12=0, 𝑥-3𝑦+6=0$. Shadow the region bounded by these lines and the 𝑥-axis. Also find the ratio of areas of triangles formed by given lines with 𝑥-axis and the 𝑦-axis.

Represent the following system of equations graphically and comment on solutions: $x+y=2; 2x+2y=4$.

Draw the graph of the equation $x=3$ and $4x=3y.$ Find the area of the figure obtained.

Draw the graph of the equation $x=3$ and $4x=3y.$ Shade the region obtained

Solve graphically: $y=\frac{3}{2}x+3; 3x+2y=14$.

Solve for $x$ and $y$: $x-3y-3=0 , 3x-9y-2=0$

Show graphically that the system of equations 

$3x-y=2$

$9x-3y=6$

has infinitely many solutions.

Draw a graph of this equation: 

$y=\frac{7x}{2}+14$

Explain no solution, unique solution and infinitely many solutions.